Part I
Preparation
There are multiple ways to make money with tube submits. The basic concept is to submit the sponsor videos to tubes and get traffic/sales using the watermark and using the backlinks (sometimes banners also) placed under the video.
The best part about tube video submitting is that we don’t need any fancy hosting, because the videos will be hosted on the tubes and the traffic you will burn is absolutely minimal!
So as with any promotion the first thing we need to do is to choose the sponsor or sponsors and contact them. We need to contact them because we want to edit their videos and not every sponsor is okay with that.
There are many ways you can edit the videos:
– you can add an additional watermark with a redirection link (e.g. www.domain.com/PAYSITE where if the surfer types in the url he will be redirected – using htaccess or php – to the tour page)
– you can remove the original watermark and add a redirection link like mentioned above (WARNING: ask for permission first!)
– you can remove the original watermark and add a new watermark where the domain will be a copy of the tour page (WARNING: ask for permission first!)
As you can imagine the best option is the 3rd one where the surfers may bookmark your landing page and you won’t loose any sales. Of course not every sponsor is ok with removing their original watermark, but there are many which can use some additional sales 🙂
Tips
– Always contact your sponsor: don’t try to watermark their videos without asking! Tube submitting is a long term business, I still receive sales from 2-3 year old submits!
– Don’t overdo the watermarking: put only ‘stylish’ watermarks on your videos, otherwise the tubes may not list you!
– Write meaningful titles and descriptions: as you may already know, search engines love tubes; a little SEO can rank you higher!
What tools do we need?
Here is the short list of tools you will need:
Tube Sites Submitter – our main tool, you can automatically create profiles and you can automatically submit videos to tubes. Some tubes require manual attention (around 5%).
Chameleon Confirmer – this tool will confirm all the mails you will receive after the profile creation. (not necessary, but will save you a lot of time)
Windows Movie Maker, Video Charge, Sony Vegas… – a video editing software of your choice. You can find free and also paid ones on the internet.
Nifty Stats – used for tracking sales statistics: clicks, hits, ratios, no. of sales etc. This tool will save you a lot of time and will give you a nice overview about your overall progress. (free and paid versions available)
As you can see most of the software is free of charge and the amount for the paid one can be covered by only one PPS sale.
Part II
Method
First you need to know that I’ve created the videos using the third option, so by removing the original watermark and adding a watermark to my own domain where the copy of the tour page can be found with a little tweak: I’ve removed the WMV trailers from the tour, so only thumbnails and episode text is available for the surfer. This way the ratios are better and you can also save a lot of bandwidth. And finally the join links will lead the surfer to the original join page.
Facts
Amount of submitted videos: 20
Average time of one submission:
– manual part: 10 minutes
– auto part: 40-50 minutes (highly depends on the connection speed and video size)
Traffic source: (mostly) type-in traffic and clickable links/banners from tubes
Length of the videos: 3-5 minutes
Size of the videos: 17-40 MB
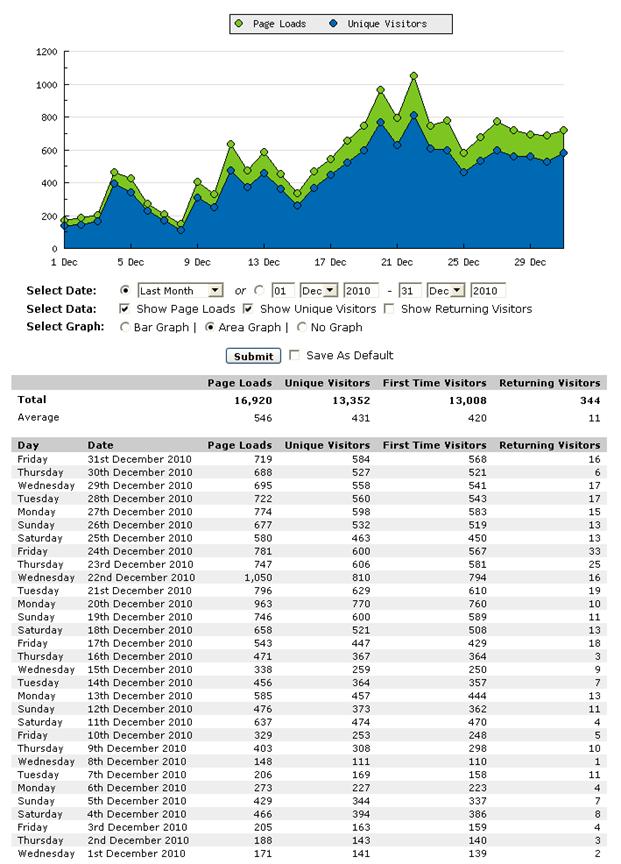
Stats, stats, stats … and some nice graphs
Let’s see some numbers. I’ve tracked my progress for 31 days (December). The traffic varies, the reason for this is that most of the tubes don’t list the videos right away and some of the tubes won’t list your video on the first page, but you will still receive traffic from these sites if you properly optimize your titles and descriptions (surfers love to use the search function, not like webmasters J ). But as you can see the traffic is rising and the site gets more then 500+ unique daily only from video submits!
Traffic screenshots:
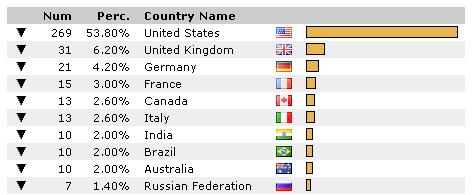
Traffic by country:
So we got traffic, but are these surfers coming from? Let’s check it out:
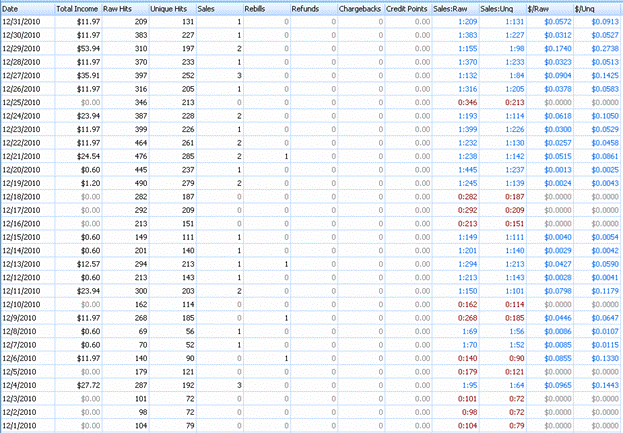
Sales screenshots:
Okay so we got traffic from so called ‘high quality’ countries. But are these people buying anything? Yes they are! Just check out the following screenshot from Nifty Stats.
I’ve tried two different join pages – one with trial and one without trial. After two weeks of testing I’ve switched back to the non-trial & non-recurring join page from the trial join page. It is the most profitable option in the long run (the member area isn’t updated anymore so there is no reason for the surfers to renew).
As you can see I’ve made 3 sales on the fourth day which is an excellent result, not talking about the constant sales after this day (with some exceptions).
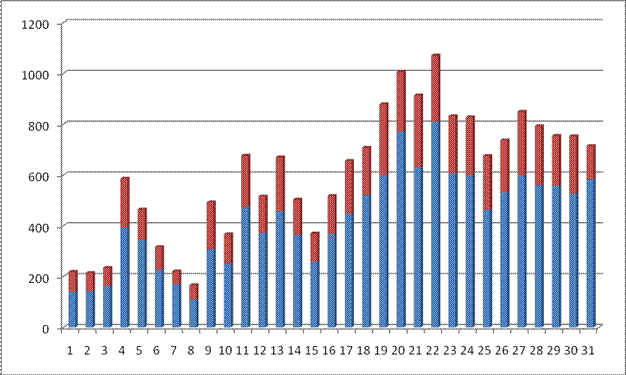
Tour page ratios:
Now you might say that these ratios are only join page ratios because the traffic to tour page isn’t tracked by the sponsor only the join hits are. Let’s compare those both. In the following graph the blue bars represent the number of unique visitors to the join page and the red bar represents the amount of unique visitors to the tour page. As you may see most of the surfers do click through to the join page:
From all these statistics we can easily calculate the overall ratio (sales : tour page unique) à 1:445
Conclusion
Submitting to tubes is an effective way to get more traffic and more sales. It’s a vital option for both affiliates and sponsors. As you can see on the screenshots above, I’ve made a pretty nice profit on my initial investment 🙂

Hi, just wanted to verify with you:
1) am I able to submit freehosted tube videos from one of my sponsers without having my own website?
2) is there a smaple version of the tube submitter I can download to get an idea of how it works?
thanks
To Chris MacMullen:
1) You don’t need to have a website because you don’t host the videos. However if you want type-in traffic then it’s good to have your own domain/subdomain (for redirection)!
2) There are tutorial videos available here also if I’m correct a demo version will be released (but don’t ask when). However the tutorial videos should give you a feel about how it works..
What’s the best way to encode video?
Codec, contaiter, bitrate, resolution…
To Restman: The video settings vary a lot and it’s hard to find the right balance. Some tubes love long videos, but some don’t. This goes for the video size also. Also its very niche specific. Amateur/homemade tubes are ok with low quality vids but pornstar tubes don’t.
I usually submit WMV videos with ~640px on the width and around 1mbit
“Traffic source: (mostly) type-in traffic and clickable links/banners from tubes”
In Submiter I not found option for add “clickable links/banners”
How to this?
To RestMan: On the video page at the software you have a ‘Site Information’ part with a ‘Site URL’ box.. There you should enter the url… many tubes don’t allow a backlink but many do and google loves those backlinks!
there’s no proof this will increase traffic or earnings without the real ability to actually click through the video or backlinks via a real tracking code.
to assume people will type in the watermark they see is ridiculous. if you actually do get any traffic, it will be very little. most surfers will do what’s easier – click the next video.
this program is also worthless if it cannot add a watermark for you.
This makes sense. I like the concept.
can you give me list of sponsors that allow watermark alteration? thanks!
are these stats generated by 20 movies submitted once or 20 movies daily?
Howdy! This is my first comment here so I just wanted to give a quick shout out and say I
truly enjoy reading your articles. Can you suggest any other blogs/websites/forums
that ccover the same topics? Many thanks!
Good post. I learn something new and challenging on websites I stumbleupon every day.
It’s always interesting to read content from other authors and use something from
other sites.
hey hi i like this article. I have been making money from adult tube websites for almost 3 years now and i am averaging about $2000/month. You can check out my method here:
http://makemoneyadultcontent.com/my-journey-to-3500-per-month-from-adult-tube-websites/
Would love to get your inputs on my methods
I have a tube web site last month i have get 800 click but not sales . Please some one suggestions me here my web site : http://luckyporntubes.com/
I have 50,000 + video
I want to make porn tube site
I can help you contact me
Hi
Good article. I gain knowledge of impressive new and demanding on websites Every day.It’s always attractive to read substance from
You can always make good money from tube sites. Proper knowledge and perfect execution is very important to make it work.
Thanks a sharing these methods, Really appreciate it.
I am interested in your software because I also want to start promoting my tube website using video uploads. Thanks for the informative very precise.
These stats are from 2010 not 2018?
Explain?
After browsing tube sites and all what I could see is really bad quality and a lot of redirects, which is annoying a lot. Than I searched for adult review sites and I might say it helps a lot. Rather to read about the best porn tube sites and after decide what tube site suites the best, then clicking around on low quality ones.
I can really recommend https://www.sensexion.com/ as a great adult review site without ads and unnecessary redirects not only for the best tube sites but also for the best live sex cams, the best dating sites and pornstars in general.
Great points. Although making money from tube sites isn’t that easy nowadays. You might also find this informative. http://adent.io/start-porn-site-make-money-porn-sites/
Hello friend.My website is not porn related,but i was interested when i saw your link on quora.com
Please could you assist on how to market my lingerie store.www.lingerie-hub.com
It is hard getting traffic to make purchase on this site.Please help me i’m a beginner
First Of all, Thank you for the helpful article I have been making money from adult tube websites for almost 1 year. you can check my new website https://www.bestfeetporn.com
Hello i have a tube with lots of contents the website is mainly about Butt Plugs
https://buttplugworld.com/
If you are interested in videos from content creators and uploaders you can send us your site https://www.tubesitessubmitter.com/blog/news/suggest-tube-site-will-send-thousands-videos-users/
We have a nice deepthroat video tube here:
https://deepthroatedtube.com/
site not working
Please ad this tube site to list https://9vids.com/ Thank you!